The fed-batch technique is an important biotechnological process strategy. Unlike the simpler Batch strategy, the substrate for microbial growth is not administered all at once but added over time. This allows control over the culture growth and product formation, whilst avoiding reactor limitations. Despite these advantages, a fed-batch will require optimization, which can present its own challenges.

This article shows one possible strategy to optimize a fed-batch. However, the topic is highly controversial, and many experts will recommend a different approach. The shown procedure is labour intensive but usually leads to success. Additionally, the gained strain characterisation can be used for further optimization, scale-up, risk analysis and a quality by design approach.
1. Define the goal
Each optimization process needs a defined goal. Assuming a recombinant protein shall be produced, the typical objective for the optimization is to reach the highest possible amount of product in the shortest possible time – hence maximizing the product time yield. This article demonstrates a possible strategy to achieve this goal. For any other goal, the shown strategy may be altered accordingly.
2. Characterize the growth of your strain
The growth behaviour is strain dependent and must be known in order to thoroughly master a fed-batch. The growth can be characterised using the following key figures:
- µmax Maximum specific growth rate
Grams of new biomass produced by one gram of biomass per hour, when the substrate is unlimited (→ batch)
- Yx/s,max Maximum yield biomass/substrate
Grams of new build biomass when one gram of substrate is consumed, and the substrate is unlimited (→ batch)
- ms Specific rate of substrate consumption for cell maintenance
Minimum amount of substrate consumed per gram of biomass per hour in order to survive
These figures can be seen as constant for a strain providing the cultivation conditions including substrate, pH, temperature, etc., do not change. The values for µmax and Yx/s,max can be obtained from batch data (Fig. 1). The value for ms, requires data from several fed-batches which may not be readily available, therefore literature values are commonly used instead.
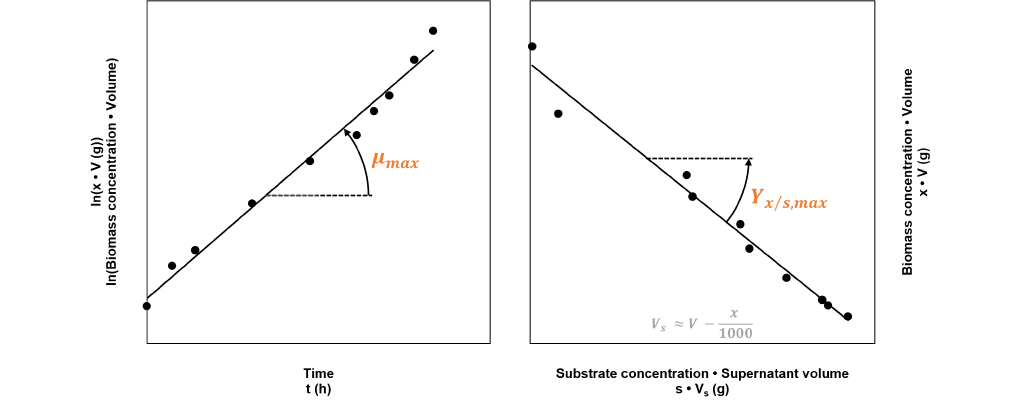
Fig 1: Calculating growth relevant kinetic figures from batch process data. The regression line’s slope on the left graph, corresponds to the maximum specific growth rate µmax. The slope of the regression line in the right graphic corresponds to the negative value of the maximum yield biomass/substrate Yx/s,max.
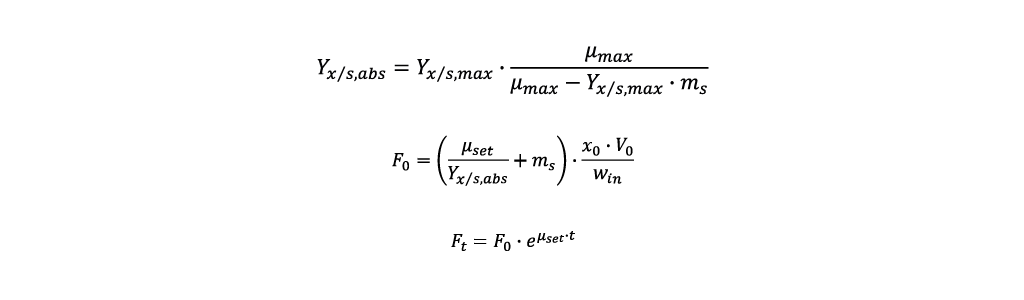
Using these values, it is possible to calculate the feed rate required to reach a desired specific growth rate µset in a fed-batch:
- First the asymptote value for the yield biomass/substrate Yx/s,abs is calculated.
- With Yx/s,abs the starting feeding rate F0 can be calculated. Additionally, the biomass concentration x0 and cultivation volume V0 at the start of the fed-batch and the substrate concentration in the feeding media win are required.
- To reach a constant specific growth rate, the temporal course of the feeding rate Ft is calculated by the following equation, where t is the time elapsed since the fed-batch started.
3. Characterize the product formation of your strain
The productivity of the strain is characterised by the specific product formation rate qp, which corresponds to the amount of product produced by one gram of biomass per hour. The value of qp is not constant, but highly dependent on the specific growth rate µ. The dependency is different for each strain and must be determined empirically. At least three fed-batch processes, each at a different µset, must be carried out to give an accurate characterisation. Fig. 2 shows how the process data can be used to calculate the reached growth rate and specific product formation rate, and details how the dependency of these two figures can be approximated.
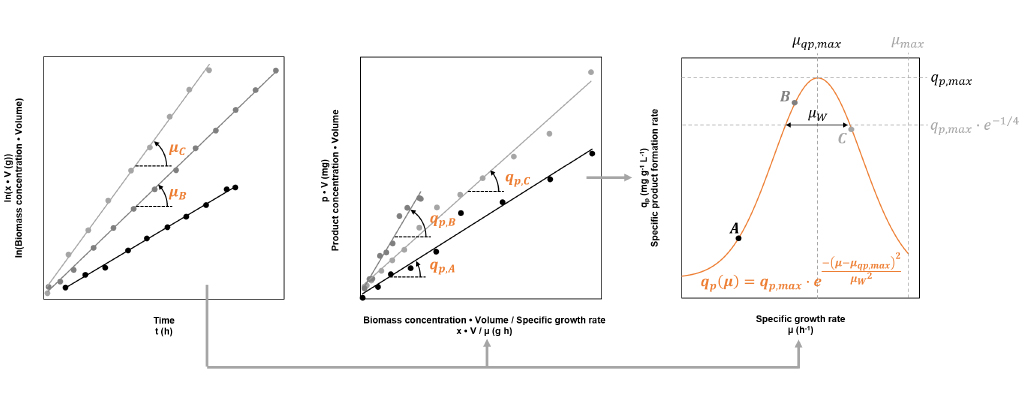
Fig. 2: By using process data from three fed-batches A, B and C, each conducted at a different but constant set specific growth rate µset, the strain’s specific product formation rate qp can be characterised. The first two graphs show how the reached specific growth rates µ and reached values for qp can be gained by the means of linear regression. The third graph illustrates a model describing the dependency between qp and µ. The fitted model reveals the specific growth rate, which leads to the highest specific product formation rate (µqp,max → qp,max).
4. Optimize the fed-batch
Rapid proliferation, high productivity per biomass and high biomass concentration are all prerequisites to maximize the product time yield. The dilemma is that they cannot be achieved at the same specific growth rate (Fig. 3).
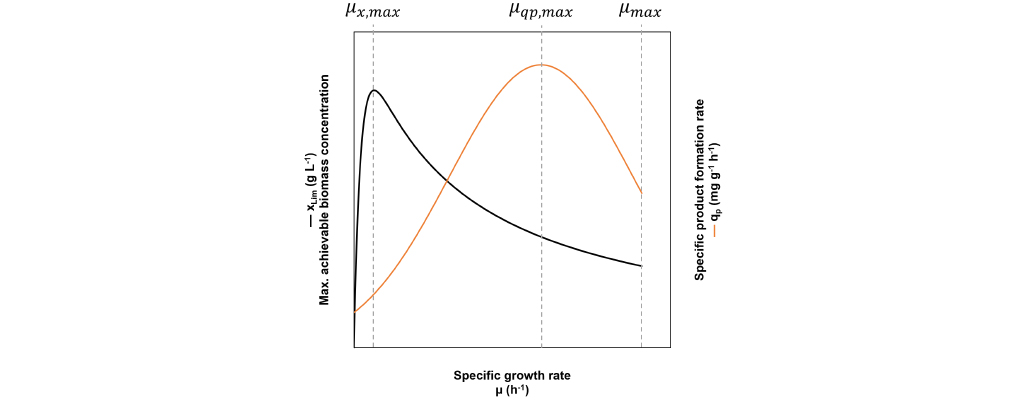
Fig. 3: In a fed-batch the specific growth rate µ can be freely chosen. At µx,max the maximum achievable biomass concentration xLim is at its highest, but the growth speed is very slow and depending on the strain, qp is not necessarily high. At µqp,max the specific product formation rate reaches its maximum qp,max, but xLim and the growth speed are not necessarily high. Finally, at the maximum specific growth rate µmax the cell proliferation is at its fastest, but xLim is low and the specific product formation rate is not necessarily high.
This predicament is the reason why a fed-batch requires an optimization. It can be solved by temporal segregation into three phases, each with a different goal:
Batch phase → Maximized biomass proliferation
A rapid biomass growth is achieved by introducing a batch phase prior to the fed-batch. As the substrate is available in abundance, the microorganisms will grow at the maximum speed characterised by the maximum specific growth rate.
Defining the batch’s volume and concentration is an optimization issue of its own. In general, we recommend the following procedure:
- Substrate: if the specific product formation rate is close to zero at the maximum specific growth rate (Fig. 3) and the maximum specific growth rate is low compared to other substrates, it is worth using a substrate with a higher µmax during the batch phase. This is often the case for Pichia pastoris, where the batch is conducted with glucose for rapid proliferation, while methanol is used during the fed-batch to induce the AOX promoter driven product formation.
- Substrate concentration: For most organisms (or organism classes) standardized batch media containing balanced levels of compounds exist. It is not advisable to change the substrate concentration in this type of media, as it may lead to limitations or excesses in other compounds. Instead, it is recommended to use a standardized batch medium with a regular amount of substrate whenever possible. If modifications are nevertheless necessary, the rule is: the higher the starting substrate concentration s0, the shorter the whole process will last – but the amount of product will decrease.
- Volume: To maximize the product quantity, the reactor must be filled completely by the end of the fed-batch. The easiest way to achieve this is by using an empirical approach. For the first run the starting volume is set to the minimum working volume of the reactor Vmin. The volume at the end of the fed-batch is measured and defined as Vend. The required starting Volume V0 to reach the maximum working volume Vmax by the end of the process, can then be calculated as follows:
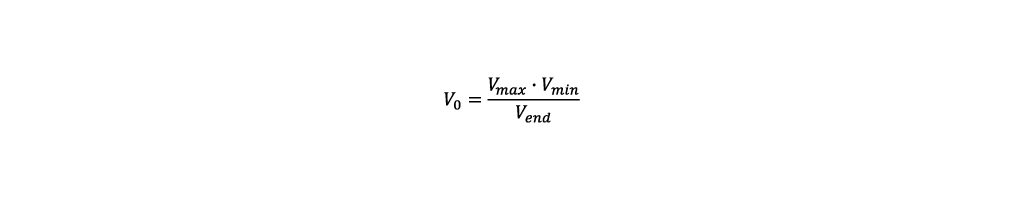
Exponential fed-batch → Maximized productivity per biomass
Once the substrate from the batch has been depleted, an exponential fed-batch is started. Since the biomass concentration is still comparably low and will only increase over time, a high productivity per biomass is emphasised. Therefore, the fed-batch is carried out at the specific growth rate resulting in the maximum specific product formation rate (µqp,max → qp,max). If µqp,max is greater than 80% of µmax, the specific growth rate is set to 80% of µmax to avoid substrate accumulation.
pO2 dependent fed-batch → Maximized biomass concentration
Eventually, the bioreactor’s limits for cell maintenance will be reached. In lab scale, this typically means that the media’s oxygen saturation pO2 will drop to zero. A very low pO2 can alter the metabolism or even the product quality. This can be circumvented by defining a lower boundary for the oxygen saturation pO2L, which should not be undercut.
When pO2L is reached, it is possible to reduce the set specific growth rate to allow for a further increase of the biomass concentration without causing an oxygen shortage. However, this will also decrease the specific product formation rate. Therefore, the specific growth rate should only be reduced gradually, with each step trading a reduction in the specific product formation rate for a higher biomass concentration (Fig. 4). The easiest way to achieve this is to combine the exponential fed-batch and the pO2 dependent fed-batch into one feeding algorithm:
- For the first iteration the initial feeding rate Fstart is calculated. In this case x0 is the biomass concentration after the inoculation.
- Afterwards, the feeding rate is modified depending on the pO2 value, where Ft is the current, Ft-1 the last feeding rate and Δt the time elapsed between the two.
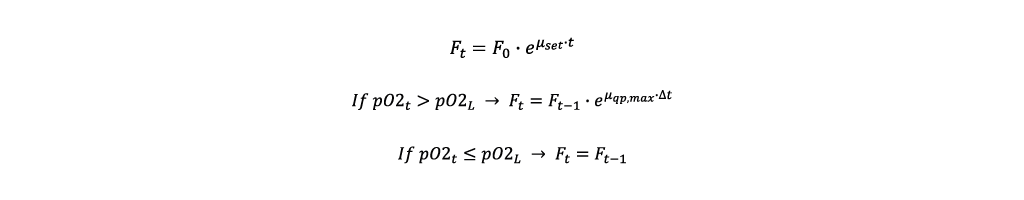
The process will conclude when the pO2 decreases despite a constant feeding rate has been reached (Fig. 4). At this point, any further increase of the biomass concentration will cause an oxygen shortage.
It must be highlighted that for larger reactor types, the limiting factor may be the heat dissipation instead of the pO2. Therefore, the temperature will permanently increase above the setpoint. In this instance, the shown strategy can be altered accordingly.
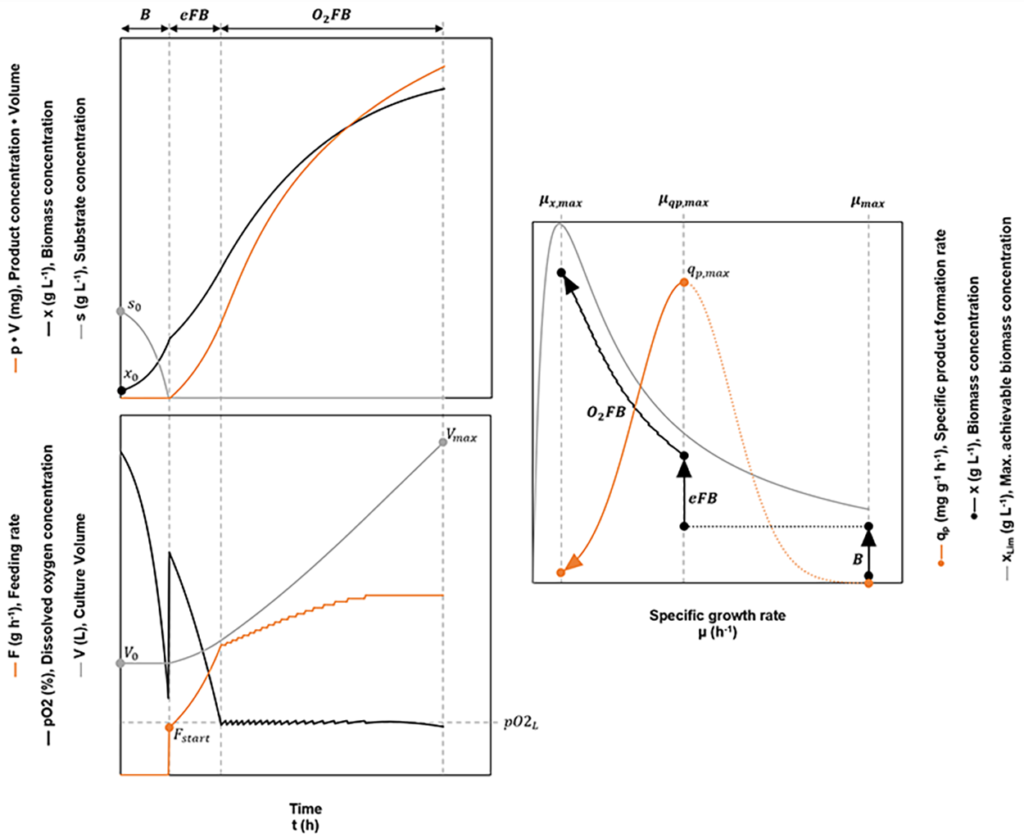
Fig. 4: Schematic overview of an optimized fed-batch. During the initial batch phase B, the culture grows at the maximum specific growth rate µmax. When the initial substrate s0 is consumed completely, the exponential fed batch eFB is started, which is conducted at the specific growth rate leading to the maximum specific product formation rate (µqp,max → qp,max). As soon as the dissolved oxygen concentration drops below a given lower limit pO2L, the pO2 dependent fed-batch O2FB is started. The process ends when the pO2 drops below pO2L, despite a constant feeding rate. Ideally at this point, the reactor’s maximum working volume Vmax will have been reached.
5. Consider further modifications
If the resulting bioprocess does not lead to a satisfactory result, the set specific growth rate for the exponential fed-batch can be altered. Reducing it below µqp,max will potentially lead to a higher amount of product but will increase the process duration. Alternatively, an increase will lead to a shorter process duration, while reducing the yielding amount of product.
Summary
- Optimizing a fed-batch is labour intensive. Therefore, it is important to have a proven strategy to make the time invested worthwhile.
- This article shows one possible strategy to maximize the resulting amount of product in the shortest possible time. If needed, it can be altered in order to match another goal.
- The key to success is to divide the process into phases, each with a different goal and to set the specific growth rate according to the goal of each phase.
Nomenclature
| µ | h-1 | Specific growth rate |
| µmax | h-1 | Maximum specific growth rate. Reached at unlimited growth (batch) |
| µqp,max | h-1 | Specific growth rate which leads to qp,max |
| µset | h-1 | Set specified growth rate for a fed-batch |
| µw | h-1 | Width value of the qp(µ) dependency |
| µx,max | h-1 | Specific growth rate which leads to maximum biomass concentration |
| F0 | g h-1 | Initial feeding rate |
| Fstart | g h-1 | Initial feeding rate for the optimized fed-batch |
| Ft | g h-1 | Feeding rate at time t |
| ms | g g-1 h-1 | Specific rate of substrate consumption for cell maintenance |
| pO2 | % | Dissolved oxygen concentration in medium |
| qp | mg g-1 h-1 | Specific product formation rate |
| qp,max | mg g-1 h-1 | Maximum specific product formation rate |
| s | g L-1 | Substrate concentration |
| s0 | g L-1 | Substrate concentration at the time of inoculation |
| t | h | Elapsed time since fed-batch started |
| Δt | h | Elapsed time between two iterations |
| V | L | Volume of cultivation broth |
| V0 | L | Volume of cultivation broth after inoculation |
| Vend | L | Volume of cultivation broth reached by a characterisation fed-batch conducted with V0 = Vmin |
| Vmax | L | Maximum working volume of the reactor |
| Vmin | L | Minimum working volume of the reactor |
| Vs | L | Supernatant volume |
| win | g g-1 | Substrate content in the feeding medium |
| x | g L-1 | Biomass concentration |
| x0 | g L-1 | Biomass concentration after inoculation |
| xLim | g L-1 | Maximum achievable biomass concentration, limited by the oxygen supply of the reactor |
| Yx/s | g g-1 | Yield biomass/substrate |
| Yx/s,abs | g g-1 | Asymptotic value of the Yx/s(µ) dependency |
| Yx/s,max | g g-1 | Maximum yield biomass/substrate. Reached at unlimited growth (batch) |
| B | – | Batch phase |
| eFB | – | Exponential fed-batch phase |
| O2FB | – | pO2 dependent fed-batch phase |

Simin Hagh Nazari
It is very good and useful.
mferndriger
Thank you for your kind comment. I am happy our article was helpful to you. BTW: loved your paper on cold plasma modification of starches.
fanming yang
for research
mferndriger
Thank you for the feedback. Yes, you are right. In industrial environments processes usually stick to standard protocols instead of being developed from scratch. Standard protocols however are commonly based on similar approaches as described in the article. For example, the often-used Pichia fermentation process guidelines from Invitrogen contain a batch followed by an exponential fed-batch and a linear or constant fed-batch.
Olivier Berteau
Thanks Iwo for sharing this article. I would be happy to discuss with you understanding your MS&T background. Hopefully, I will be able to share some additional insights to support this article. Best regards, Olivier
Chantal Fiechter Schaub
We'll keep in touch, Olivier.